Optimisation in Data Science – Mathematical v’s Machine Learning approaches

Written by Alex Essebier, Vivian Mai and Sahil Bahl

Most organisations face everyday problems that can be solved faster and more accurately by machines. A prime example is the area of logistics which includes staff rostering, supply chain management, delivery route planning, warehouse management and more. In this blog, we will explore computational approaches available to assist businesses in managing their resources to achieve the optimal outcome for their customers, staff and the business.

There are two main computational approaches used to solve logistics problems: mathematical optimisation and machine learning. Mathematical optimisation takes the approach of exploring all options to prescribe the optimal (i.e. best) solution while machine learning attempts to predict the ‘best’ solution based on historical data. Here we look at each approach independently then explore how the two can be used collaboratively to achieve the best outcome.

What types of problems are suited to optimisation?

Optimisation aims to quickly and accurately provide the best solution to a problem. Problems suited to being solved in this way are generally well defined, constrained and can be easily represented using expert knowledge. So much so that optimisation problems can be represented by a ‘digital twin’ or a virtual representation of the system in question. Some examples of problems well suited to optimisation include:

• Route planning (last mile delivery, transport)
• Rostering/scheduling (shifts/hours/staff)
• Warehouse logistics (how to layout a warehouse for best efficiency)
• Supply chain logistics (what to order, when and where from
• Manufacturing pipeline design (how to maximise efficiency and output of manufacturing equipment, how to know which equipment to buy)
• Urban development

Optimisation can help answer long term, big picture questions like where should a road be placed or how a warehouse should be organised, but it can also help short term business decision making. For example, how should the roster change if a staff member is sick or what impact a delayed stock delivery will have.

Overall, optimisation assists businesses in making the best use of their resources to solve a problem.

So how do we solve optimisation problems? Let’s start with a problem

The Travelling Salesperson Problem (TSP) is a simple and well researched example of route optimisation. Simply, a salesperson needs to visit a number of towns and we would like to find a route that has the lowest cost while taking them to all stops starting and finishing at the town in green. In this scenario, cost is influenced by salary (total time) and fuel (distance travelled) and the overall aim is to minimise cost.

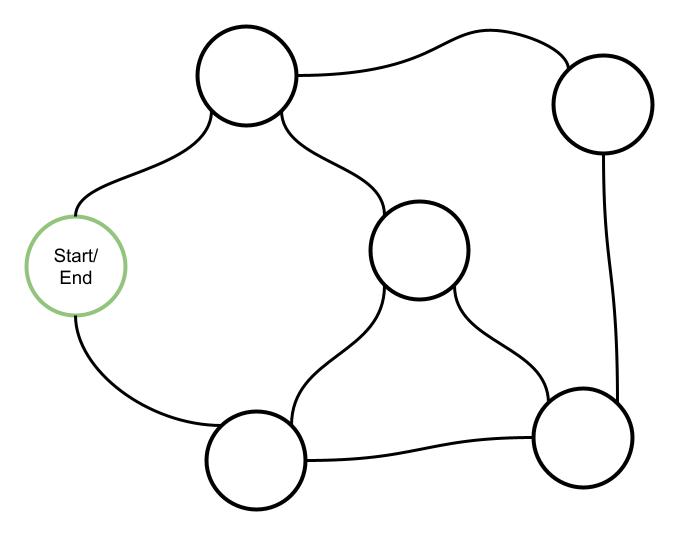
Without any additional information other than knowing whether a road exists between two towns, it’s easy to find one of the quickest routes as highlighted in blue. However, in reality, each road can be measured with distance and time as variables. (Assume distance and time are proportional). When we consider the distance between towns, our original blue route is a distance of 73km while the new route in orange is a distance of 62km.

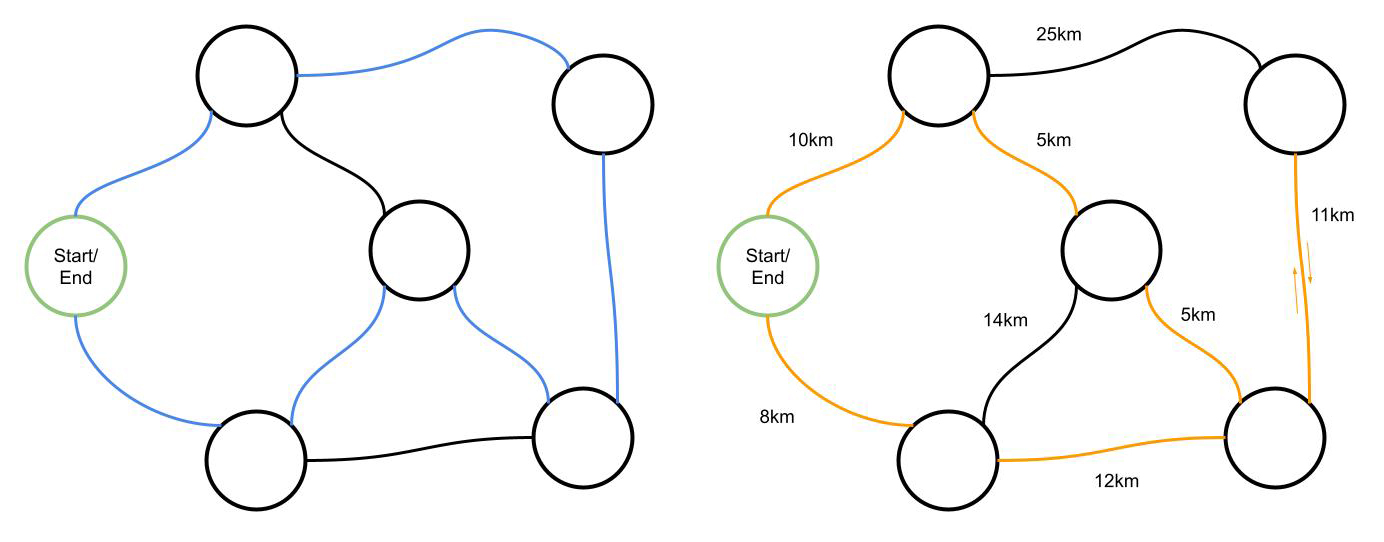
With no other requirements, the salesperson could complete the route in either direction with an equal distance. If distance and time are not proportional (e.g. influenced by road rules or traffic) we may find a different route again as optimal because while it may not minimise distance, it does minimise time and satisfy our overall goal of minimising cost (assuming cost of salary is greater than cost of fuel <insert joke about obscene fuel prices :P>).

Next, consider if our salesperson had to be in town A in the morning and town B in the afternoon. This is an example of a constraint and determines the direction of the optimal route. As this constraint must be met, it is considered a hard constraint and any routes that don’t satisfy this requirement are non-feasible.

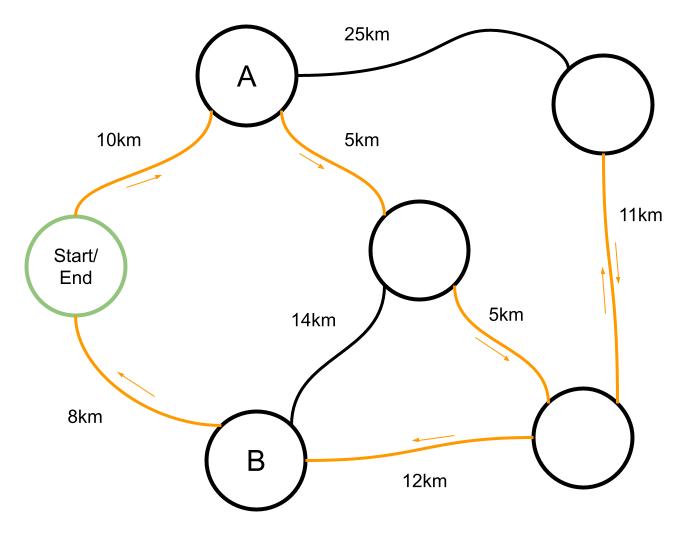
In comparison, an example of a soft constraint would be whether the trip takes more than 8 hours as our salesperson needs to be paid extra for every hour of work over 8 hours. A soft constraint doesn’t rule out a route if it takes more than 8 hours, but it does incur a penalty in that it costs more to pay the salesperson. Soft constraints can be considered more as goals.

With this example scenario that has a small number of variables and constraints, it would be easy to document all possible routes and associated costs and determine which has the lowest cost: i.e find the ‘best’ or ‘optimal’ solution. However, in most real-world scenarios there are a large number of variables and constraints leading to potentially millions of solutions making it challenging and time consuming for a human to solve the problem without the support of a computer. Luckily, there are a variety of algorithms and computational solutions that can be applied to identify optimal solutions.

What is mathematical optimisation?

Mathematical optimisation aims to generate all possible solutions to a problem, assign a value to each and select the solution with the minimum or maximum value, i.e. the optimal outcome. In the above example, a computer could achieve this more quickly and accurately than a human is able. In the real world, you would be dealing with multiple staff, more towns to visit, a larger number of constraints and many other factors. This results in a number of possible routes so large that it would take the most powerful computers available decades, if not centuries, to identify all possible routes and select the optimal one.

To combat this, mathematical optimisation approaches rely on heuristics to find the optimal solution without having to search through all possible solutions. These heuristics and the improved power of computers has resulted in complex optimisation problems being solved in reasonable amounts of time, but there is still room for improvement.

Some examples of mathematical optimisation algorithms include:

• Genetic algorithms
• Ant colony optimisation
• Local search algorithms
• Simulated annealing
• Bayesian optimisation

What is machine learning?

While mathematical optimisation is quite targeted in its applications, machine learning is a much broader field that is applicable to a larger number of problems beyond optimisation. Machine learning lacks a clear definition but is based on the concept that computers can examine large amounts of data, identify patterns or trends and make predictions.

Generally, machine learning problems can be grouped by outcomes such as:

• classification; labelling data points with an outcome,
• clustering; grouping similar data points,
• and regression; finding the relationship between a dependent and independent variables.

Problems solved using machine learning do not need to be as well defined or constrained as problems that can be solved using mathematical optimisation. In fact, the search space for a machine learning problem often includes a large number of variables (or features) with numerous unknowns or aspects of the problem that cannot be measured, recorded or defined in a way that a computer can interpret. Consider weather forecasting and the limitations around measuring all atmospheric pressures and temperatures to create an accurate model.Or facial recognition, where a mathematical representation of a face does not exist.

To use traditional machine learning to solve the Travelling Salesman Problem, we would assume that our salesman has been making similar trips over a period of time, maybe to slightly different sets of towns resulting in different routes. We would collect all examples of how the routes had been solved previously and pass this data to a machine learning algorithm. This algorithm would then use its knowledge of previous routes to predict a new route. There is no guarantee that this prediction will be the best and most accurate solution making it harder for businesses to rely on the output from traditional machine learning.

Examples of machine learning approaches include:

• Regression
• Random forest
• Neural networks
• Deep learning
• Computer vision

Machine learning approaches generate predictions that aim to generalise as the resulting models are applied to scenarios which have never before been observed while optimisation problems fit the solution to the search space. Therefore, while possible, traditional machine learning is not considered an ideal solution to solving optimisation problems.

Where mathematical optimisation and machine learning can work together

To explore how DS/machine learning and optimisation can work together to solve problems such as last mile delivery or rostering, let’s explore a new problem: staffing a call centre. For this example, our aim is to ensure enough staff are available to minimise wait times for customers but also minimise time staff are idle. This will allow us to serve our customers at the lowest cost to the business.

Assuming that you know key variables and constraints such as:

• The shift schedule and how many employees need to be on each shift based on:
  • Expected call volumes
  • Average time taken to respond to a customer
• How many employees are available
• How many hours a week each employee can or needs to work (based on contracts)

Then this information can be fed into a mathematical optimiser to assign staff to shifts in the most feasible way.

To solve this problem using traditional machine learning, you would need historical examples of how staff were assigned to shifts that the algorithm can learn from to allocate the next set of shifts. The output from examining the historical data would be a prediction of what the next best shift assignments would be. This prediction could help guide you in deciding the best shift assignment but isn’t well equipped to handle the intricate sets of decisions that dictate shift assignments in the same way optimisation can.

As a machine learning model is based on historical data, the model is limited to past examples in finding the most optimal roster that exists while an optimiser looks at all possibilities for the next roster. Further, if there are any changes to the system such as staff being sick or call volumes suddenly changing, the resulting model may no longer be valid while an optimiser would easily adapt to the new information and regenerate a feasible roster.

One exciting new field of machine learning research that could be applied to help solve this problem is reinforcement learning however, this is a topic for another blog!

Machine learning to intelligently reduce the search space

The use of an optimiser has significant advantages over traditional machine learning predictions when solving our call centre problem, but this does come at a cost. Examining all possible roster combinations to find the optimal solution is computationally expensive and time consuming. Most optimisation approaches employ heuristics or metaheuristics to find an optimal solution without exploring all possible solutions.

Another way that machine learning can positively augment optimisation is by intelligently reducing the search space explored by an optimiser to boost the speed of the algorithm and provide accurate results more quickly. Machine Learning can be applied to classify some combinations of shift assignments as bad, preventing the optimiser exploring those combinations any further resulting in shorter run times. Similarly for the problem of delivery route planning, machine learning can be employed to ensure that routes which won’t result in the best outcome are identified early and removed from the search space to improve run times.

Machine learning to set constraints for optimisation

Where machine learning is currently most valuable is when an expert needs help in setting the constraints that are fed into the optimiser. There are a number of business inputs that can be forecast or predicted depending on the business problem and the accuracy of these inputs plays a critical role in arriving at the optimal outcome. Specifically, using our call centre as an example:

1. A machine learning model could be trained on historic call volumes, call duration and customer wait times to learn how many staff should be rostered on and at what points during the day
2. A machine learning model could be used to forecast call volumes over a period of time to help allocate more or fewer resources as required
3. A machine learning model could forecast staff absences and assist in predicting whether additional staff should be on call

The result of these models would be a reduced set of inputs into the optimiser resulting in a smaller search space allowing the optimal solution to be discovered faster.

Which approach is taken by current optimisation solution providers?

Optimisation is applicable to solving logistics problems in numerous industries and, as such, has been heavily researched for decades. There are a large number of 3rd party solution providers available that solve industry specific problems using mathematical optimisation alone or combinations of machine learning and mathematical optimisation. When starting out on a journey to introduce optimisation solutions into your business, it’s smart to explore the current tools that are available.

It’s worth noting that third party solutions are tailored to solve specific problems and you may find a tool that fits your use case well; however, the tools often lack the ability for users to customise to their needs and may not be dynamic enough for unique use cases. Also, with any 3rd party tool there is always a risk

• that the solution changes and becomes non-viable for your particular circumstance,
• that your needs change and the solution is no longer valid,
• or that the company ceases to exist leaving you in the lurch.

On the flip side, custom solutions can be difficult to establish and maintain without technical expertise but they provide you with a solution that

• is fully customisable,
• flexible or dynamic, and
• owned by you.

Optimisation and machine learning solutions for your business

For businesses facing logistics type problems, there is significant value in employing a computational solution to optimise time and resources across the organisation. This could vary from staff rostering, to planning delivery routes and even to organising your warehouse to enable staff to fill orders more efficiently. There are a number of solutions available to solve these problems by efficiently identifying optimal solutions including mathematical optimisation, machine learning, or a combination of both.

Mathematical optimisation has been extensively researched for decades with a number of highly developed and robust solutions available as custom tools or from third party providers. Applying this approach is an excellent starting point when it comes to optimising your business processes. While third party providers have associated risks, it’s worth exploring what solutions are available and whether the right tool for your problem already exists.

The application of machine learning to solving optimisation problems is more recent but has made an impact when it comes to improving run times of mathematical optimisation models. You may find that there already exist third party providers that have achieved success by applying machine learning to their optimisation models. If you find that mathematical optimisation isn’t providing optimal results quickly enough, then exploring how machine learning can improve run times would be valuable.

If you don’t know where to start and you’re looking for some guidance, Mantel Group has the skills and expertise to build custom optimisation solutions which combine machine learning and mathematical optimisation to find the best solution in an efficient manner.

What is the difference between an optimisation problem and a machine learning problem? An overview:

Optimisation Machine Learning (ML)